|
Interstellar Bands Interstellar Bands
Interstellar Bands in x Per spectrum.
The light from this star is partially absorbed by the dark matter (gas and dust) that lies in the line of sight. Infact from its position into the HR diagram, we obtain an absolute magnitude of -7 and thus at a distance of 2000 light years it should still shine as a second magnitude star. But the visual magnitude is only about 4.1. The interstellar extinction factor in this case is as high as two magnitudes. The light from such a star (and of many other into the OB associations) behave like a spectrophotometer lamp that probes the chemical nature of the matter that it crosses in the line of sight.
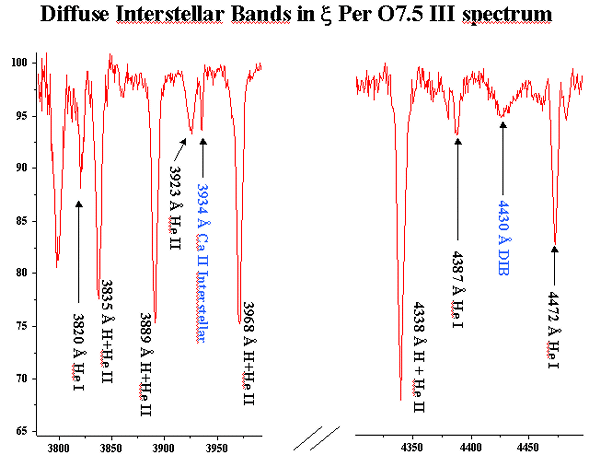
Picture 1: Selected portions of the spectrum of Menkib, 46 Per, that show the sharp and diffuse absorption bands (DIB=Diffuse Interstellar Bands) that are due to the interstellar gas and dust . Spectrum recorded with 1 ┼ resolution, 5 minutes exposure for each one of the 3 spectral windows, with 0,6 m F/20 Cassegrain telescope, grating 1800 l/mm, collimator lens f=300 mm, camera lens f=50 mm, CCD=MX5 XPress.
Looking at the spectrum of this star (see picture 1), we can see some weak bands and sharp lines that should not apperar in the spectrum of an O star that has a surface temperature as high as 30000 K.
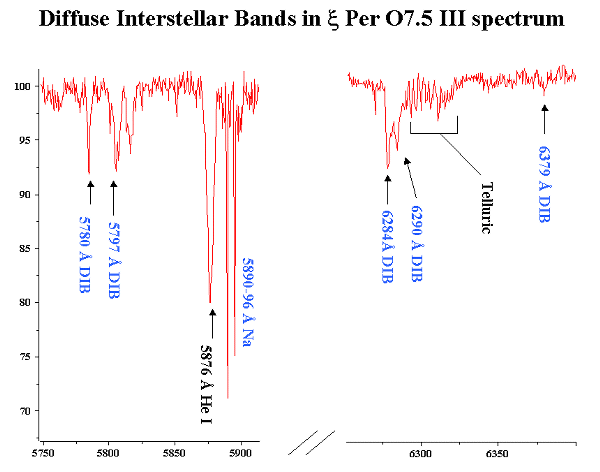
One of the strongest sharp absorbption is clearly due to neutral Sodium (doublet at 5890-96 ┼) but also sharp H and K lines of the singly ionized Calcium can be observed.
Among the diffuse bands we can recognize shallow absorptions at 3874 (CN), 3958 (CH+),4233 (CH+), 4300 (CH), 4430 , 5780, 5797, 6284, 6290, 6613 ┼.
Picture 2: Selected portions of the spectrum of Menkib, 46 Per, that show the sharp and diffuse absorption bands (DIB=Diffuse Interstellar Bands) that are due to the interstellar gas and dust . Spectrum recorded with 1 ┼ resolution, 5 minutes exposure for each one of the 3 spectral windows, with 0,6 m F/20 Cassegrain telescope, grating 1800 l/mm, collimator lens f=300 mm, camera lens f=50 mm, CCD=MX5 XPress.
Later on, also Fe I, K I and Ti II sharp lines were identified but the diffuse bands (DIB) were first discovered by Merrill in 1934 and since then, despite to many attempts, it was not possible to reproduce them in a laboratory set up.
|