SPECTROGRAPHS AND RELATED INSTRUMENTS
Spectrographs -
Entrance Optics -
CCD -
Atmosphere
- Mechanical Flexures
- Ref Lamps
Atmospheric Refraction
Light from stars must pass throught our atmosphere before entering telescope and spectrograph.
Atmosphere affect light in different ways. In this first paragraph we deal with bending of light
that unfortunately depends on wavelength of incoming light.
Differential refraction produces an height shift of the image of a star above horizon. Blue light is
deviated more than red light and thus the image of a star close to the horizon appears like a small
spectrum with blue up and red down.
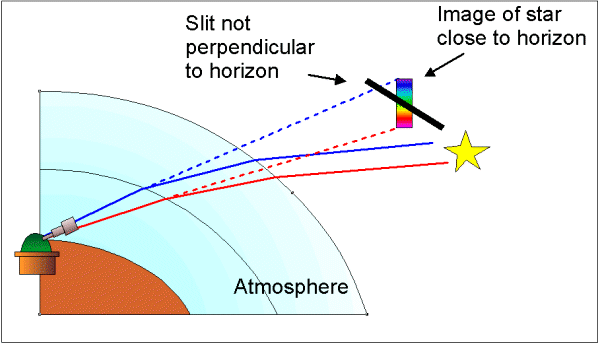
|
|
Picture 1: Refraction of light throught earth atmosphere acts like in a prism, expecially close to
the horizon and the image of a star result in a small spectrum. If the slit is not oriented perpendicular
to the horizon, this results in a wavelength selective loss of light.
|
The extent of this spectrum can be of many arcsec (picture 2) close
to the horizon and is reduced at less than 2 arcsec (from 4000 to 7000 ┼) only for height of more than
30 degrees.
When observing at less than 30 degrees above horizon, if the slit of the spectrograph is not oriented
perpendicular to the horizon, a selective loss of signal can result for blue or red part of the spectrum,
because the blue and red images of the star cannot enter the slit.
This is particularly true for big telescopes, where the slit width is always setted to a dimension comparable
to the image of the star blurring disk (2 arcsec).
Refraction index of air at SPT varies from 1.000275 @ 7000 ┼ to 1.000278 @ 5000 ┼ and as much
as 1.000282 @ 4000 ┼.
The formula that can be applied to calculate the atmospheric refraction is:
R = (a/b) x sin(z) x [(cos2(z) + 2b)1/2 - cos(z)]
where at the sea level a=(n2-1)/(2 x n2) and n is the refraction index of air.
Above sea and for temperatures different from 0░, a should be corrected by the factor (b/760)*1/(1+0.0036*T) where T is the absolute temperature and b is the barometric pressure in mmHg.
The costant b can be calculated with b=0.0025-a.
These formulae were adapted from Zagar - Astronomia Sferica e Teorica - Zanichelli.
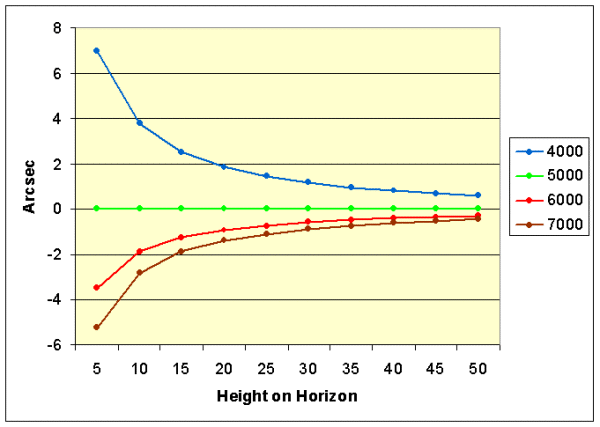
|
|
Picture 2: Refraction of light as a function of height above horizon and wavelength, compared
to green light (5000 ┼). The graph was calculated for the height of Campo dei Fiori (Varese - Italy)
observatory that is 1226 m above sea level. The light bending increases 15% at the sea level due to the
increased density of atmosphere.
|
Telluric lines absorption
Gases in the atmosphere can absorb light at selected wavelengths (mainly in Near IR from 6000 to 10000 ┼ and, of course much more in the IR).
Stronger absorptions are due to water vapour and Oxygen. Picture 3 shows the absorptions of WV from yellow to the deep red
part of spectrum with enlarged the region around Ha.
Telluric lines can be used as precise wavelength calibrators because they are in a rest reference frame (zero
Doppler shift) and because their optical path in the spectrograph is exactly the same as that of the star.
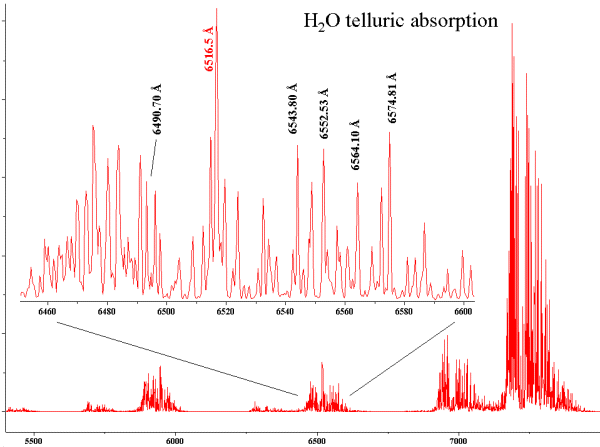
|
|
Picture 3: Simulated spectrum of water vapour lines. FWHM is 0.7 ┼. Intensity and position of each line are obtained
in the GEISA database .
The identified lines are not blended and can be used for calibration purposes around Ha.
|
|
|



